据点|流形_第一节：半监督聚类算法概述

篇首语：本文由编程笔记#小编为大家整理，主要介绍了第一节：半监督聚类算法概述相关的知识，希望对你有一定的参考价值。

文章目录

• 一&＃xff1a;半监督聚类
• 二&＃xff1a;约束信息
• • &＃xff08;1&＃xff09;标签约束
  • &＃xff08;2&＃xff09;成对约束
  • • A&＃xff1a;概述
    • B&＃xff1a;举例
    
    
  
  

半监督聚类&＃xff08;semi-supervised clustering&＃xff09;&＃xff1a;传统的聚类学习任务是一种无监督学习任务&＃xff0c;也即假设所有样本数据的簇标签未知。但是在某些学习任务中&＃xff0c;用户具有某些领域的背景知识&＃xff0c;也即约束信息。所以人们希望将这些领域知识应用到聚类任务中&＃xff0c;所以这类学习任务称之为半监督聚类。半监督聚类可以分为&＃xff1a;

• 广义的半监督聚类&＃xff1a;在实际聚类任务中&＃xff0c;相对于数据本身而言&＃xff0c;数据的约束信息是更难以获取的&＃xff0c;用户只能获取较为明显数据样本的标签&＃xff0c;或只能得到施加在样本点之间的约束&＃xff0c;所以这些信息称之为广义的半监督聚类
• 狭义的半监督聚类&＃xff1a;它只限于针对样本点的约束信息

所以半监督聚类主要研究&＃xff1a;如何利用少量的约束信息来得到更加准确的聚类结果&＃xff0c;同时不仅利用约束样本提供的信息&＃xff0c;而且考虑所有无约束样本集所隐含的结构信息

约束信息&＃xff1a;约束信息通常被认为是一种背景知识或领域知识&＃xff0c;是分析数据时已知的信息。使用约束信息时&＃xff0c;通常要对约束信息和无约束样本的关系做出一些假设&＃xff0c;常见的有如下三种假设

• 簇性假设&＃xff1a;是指数据倾向于形成分离的簇&＃xff0c;并且同一簇中的数据有相同的簇标签
• 局部性假设&＃xff1a;是指约束点与其近邻更有可能属于同一类别
• 流形假设&＃xff1a;是指同一簇的数据位于一个低纬度流形上&＃xff0c;这样聚类时就可以利用流形上的距离测度

根据约束存在方式的不同&＃xff0c;约束信息分为如下两种

• 标签约束
• 成对约束

&＃xff08;1&＃xff09;标签约束

标签约束&＃xff1a;在半监督聚类中&＃xff0c;虽然整个学习任务是无监督的&＃xff0c;但是有一部分数据的标签是可知的。标签约束就是指这种数据的已知标签&＃xff0c;它可以看成是一种子集

利用标签约束的半监督聚类算法定义为&＃xff1a;对于给定数据集$D$&＃xff0c;标签约束集$L$&＃xff0c;半监督聚类算法利用$L$中的信息将$D$中数据分配到对应的簇中

&＃xff08;2&＃xff09;成对约束

A&＃xff1a;概述

成对约束&＃xff1a;是一种指明两个实例的相对关系的约束信息&＃xff1b;成对约束由以下两个集合构成

• 必连约束集&＃xff08;must-link set, ML&＃xff09;&＃xff1a;对于两个数据点
  
  
  
  
  
  x
  
  
  i
  
  
  
  
  x_i
  
  
  xi​和
  
  
  
  
  
  x
  
  
  j
  
  
  
  
  x_j
  
  
  xj​&＃xff0c;如果
  
  
  
  
  (
  
  
  
  x
  
  
  i
  
  
  
  ,
  
  
  
  x
  
  
  j
  
  
  
  )
  
  
  ∈
  
  
  M
  
  
  L
  
  
  
  (x_i,x_j) \\in ML
  
  
  (xi​,xj​)∈ML&＃xff0c;则数据点
  
  
  
  
  
  x
  
  
  i
  
  
  
  
  x_i
  
  
  xi​和数据点
  
  
  
  
  
  x
  
  
  j
  
  
  
  
  x_j
  
  
  xj​在实际中属于同一个簇&＃xff0c;此时称
  
  
  
  
  (
  
  
  
  x
  
  
  i
  
  
  
  ,
  
  
  
  x
  
  
  j
  
  
  
  )
  
  
  
  (x_i,x_j)
  
  
  (xi​,xj​)是一个必连约束&＃xff08;must-link&＃xff09;
• 勿连约束集&＃xff08;cannot-link set, CL&＃xff09;&＃xff1a;对于两个数据点
  
  
  
  
  
  x
  
  
  i
  
  
  
  
  x_i
  
  
  xi​和
  
  
  
  
  
  x
  
  
  j
  
  
  
  
  x_j
  
  
  xj​&＃xff0c;如果
  
  
  
  
  (
  
  
  
  x
  
  
  i
  
  
  
  ,
  
  
  
  x
  
  
  j
  
  
  
  )
  
  
  ∈
  
  
  C
  
  
  L
  
  
  
  (x_i,x_j) \\in CL
  
  
  (xi​,xj​)∈CL&＃xff0c;则数据点
  
  
  
  
  
  x
  
  
  i
  
  
  
  
  x_i
  
  
  xi​和数据点
  
  
  
  
  
  x
  
  
  j
  
  
  
  
  x_j
  
  
  xj​在实际中不属于同一个簇&＃xff0c;此时称
  
  
  
  
  (
  
  
  
  x
  
  
  i
  
  
  
  ,
  
  
  
  x
  
  
  j
  
  
  
  )
  
  
  
  (x_i,x_j)
  
  
  (xi​,xj​)是一个勿连约束&＃xff08;cannot-link&＃xff09;

利用成对约束的半监督聚类算法定义为&＃xff1a;对于给定数据集$D$&＃xff0c;必连约束集$ML$&＃xff0c;勿连约束集$CL$&＃xff0c;半监督算法的目标是通过最小化聚类的目标函数&＃xff0c;利用$ML$和$CL$中的信息将$D$中数据分配到对应簇中

B&＃xff1a;举例

下图给出了一个二维空间中数据的成对约束示例&＃xff0c;包含两个簇&＃xff0c;分别用圆点和三角形表示

• 必连约束集
  
  
  
  
  M
  
  
  L
  
  
  &＃61;
  
  
  
  
  
  (
  
  
  
  x
  
  
  3
  
  
  
  ,
  
  
  
  x
  
  
  4
  
  
  
  )
  
  
  ,
  
  
  (
  
  
  
  x
  
  
  7
  
  
  
  ,
  
  
  
  x
  
  
  8
  
  
  
  )
  
  
  
  
  
  
  ML&＃61;\\(x_3, x_4),(x_7,x_8)\\
  
  
  ML&＃61;(x3​,x4​),(x7​,x8​)使用实线连接
• 勿连约束集
  
  
  
  
  C
  
  
  L
  
  
  &＃61;
  
  
  
  
  
  (
  
  
  
  x
  
  
  1
  
  
  
  ,
  
  
  
  x
  
  
  2
  
  
  
  )
  
  
  ,
  
  
  (
  
  
  
  x
  
  
  5
  
  
  
  ,
  
  
  
  x
  
  
  6
  
  
  
  )
  
  
  
  
  
  
  CL&＃61;\\(x_1, x_2),(x_5,x_6)\\
  
  
  CL&＃61;(x1​,x2​),(x5​,x6​)使用虚线连接

• 对于无监督聚类&＃xff0c;不考虑以上的约束信息&＃xff0c;由于
  
  
  
  
  d
  
  
  (
  
  
  
  x
  
  
  5
  
  
  
  ,
  
  
  
  x
  
  
  6
  
  
  
  )
  
  
  
  d(x_5,x_6)
  
  
  d(x5​,x6​) <
  
  
  
  
  d
  
  
  (
  
  
  
  x
  
  
  3
  
  
  
  ,
  
  
  
  x
  
  
  4
  
  
  
  )
  
  
  
  d(x_3,x_4)
  
  
  d(x3​,x4​)&＃xff0c;所以当$k\&＃61;2$时&＃xff0c;传统的$K-Means$方法可能会把
  
  
  
  
  (
  
  
  
  x
  
  
  4
  
  
  
  ,
  
  
  
  x
  
  
  5
  
  
  
  ,
  
  
  
  x
  
  
  6
  
  
  
  ,
  
  
  
  x
  
  
  7
  
  
  
  ,
  
  
  
  x
  
  
  8
  
  
  
  )
  
  
  
  (x_4,x_5,x_6,x_7,x_8)
  
  
  (x4​,x5​,x6​,x7​,x8​)分到同一个簇中
• 对于半监督聚类&＃xff0c;当拥有以上的约束信息后&＃xff0c;一个有效利用成对约束的半监督聚类算法会将
  
  
  
  
  (
  
  
  
  x
  
  
  1
  
  
  
  ,
  
  
  
  x
  
  
  3
  
  
  
  ,
  
  
  
  x
  
  
  4
  
  
  
  ,
  
  
  
  x
  
  
  5
  
  
  
  )
  
  
  
  (x_1,x_3,x_4,x_5)
  
  
  (x1​,x3​,x4​,x5​)分到同一个簇中

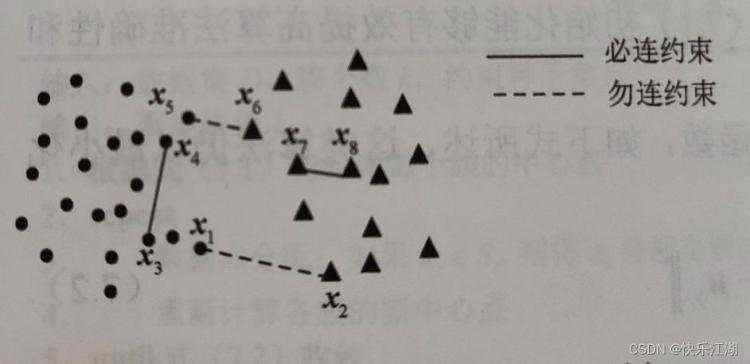
在很多实际问题中&＃xff08;例如图像检索、语音识别、GPS导航等等&＃xff09;&＃xff0c;往往难以获取数据的簇标签&＃xff0c;但是用户可以指定两个实例是否属于同一簇。在给定标签约束的情况下&＃xff0c;依然可以生成对应的必连约束和勿连约束

• 令簇标签相同的样本两两之间生成必连约束
• 令簇标签不同的样本两两之间生成勿连约束